1. Обманчивая простота
2. Ещё немного о монополии
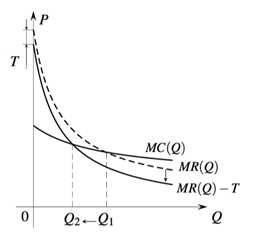
МR(Q) – это гладкая функция, которая убывает с ростом выпуска. MC(Q) тоже гладкая функция, которая убывает с ростом выпуска, но она не такая крутая, как MR(Q).
а) Напишите уравнение максимизации прибыли выпуска маршмеллоу до введения налога $(Q_1)$.
б) Напишите уравнение максимизации прибыли выпуска маршмеллоу после введения налога $(Q_2)$.
в) Скажем, что у нас есть $f(Q)= MR(Q)-MC(Q)$. Используя полученные ответы в а) и б) напишите уравнение, которое будет включать в себя $f(Q_1),\; f(Q_2)$ и $T$.
г) Докажите математически, что налог будет вести к уменьшению выпуска продукции.
3. Флэш – Производительность
- Численность экономически активного населения страны (так называемых работников) составляет 1 миллион человек и не меняется.
- В конце нулевого месяца $(t = 0)$ безработица находится на своём естественном уровне, равном $u^*= 5\%$. Естественный уровень безработицы не меняется.
- Экономика переживает спад, поэтому в начале каждого следующего из трёх месяцев $(t = 1;2;3)$ фирмы увольняют некоторое количество работников, в результате чего уровень безработицы повышается на 1 процентный пункт по сравнению с концом предыдущего месяца. При этом никто из безработных не получает предложения о трудоустройстве.
- Продуктивность каждого трудоустроенного работника в конце нулевого месяца равна 100 ед/мес, что превышает продуктивность любого безработного в тот же момент времени.
- Если работник в течение какого-то месяца является безработным, то к концу этого месяца его продуктивность падает в 1,25 раза в силу того, что он не практикуется.
- Если работник в течение какого-то месяца является трудоустроенным, то за этот месяц его продуктивность не меняется.
- Фактический совокупный выпуск $Y(t)$ в месяце t создаётся только трудоустроенными работниками и определяется как сумма их производительностей.
- Потенциальный совокупный выпуск $Y^* (t)$ в месяце t определяется как общее количество единиц продукции, которое могло бы быть произведено экономикой за месяц t, если бы безработица была на своём естественном уровне.
a) Найдите величину фактического совокупного выпуска $Y(3)$
b) Оцените сверху величину потенциального совокупного выпуска $Y^* (3)$ максимально точно.
c) Оцените величину изменения потенциального выпуска за 3 месяца с $Y^* (0)$ до $Y^* (3)$ (эффект гистерезиса).
4. Странный случай
| X | 0.5 | 1 | 2 |
| $P(X=x_i)$ | p | 1-2p | p |
При этом $Y=\dfrac{1}{X}$
а) Найдите такое $p$, при котором X=Y выполняется всегда.
б) Найдите все возможные значения $p$, при которых X и Y распределены идентично.
5. Остатки сладки
б) Найдите остаток от деления выражения $x^{2018}-2$ на $x^{253}-1$, при $x \gt 1$
6. Смерть и налоги
а) Представим, что власти решили вести налог на производителей эликсира: волшебники при ненулевом производстве должны заплатить налог T. Выведите функцию, показывающую зависимость величины общественных потерь от размера налога T.
б) Представим, что теперь государство решило ввести налог на каждую единицу произведённого товара этими колдунами в размере t. Выведите функцию, показывающую зависимость величины общественных потерь от размера налога t.
в) Рассмотрим случай, если власти решили ввести налог в $100\cdot\mu\%$ от цены. Выведите функцию, показывающую зависимость величины общественных потерь от размера налога $\mu$.