1. Товар Икс
\(\begin{equation} P_D=a-bQ \\ TC=(c+t)\cdot Q \end{equation}\)
Тогда функция прибыли имеет вид:
\(\pi = Q\cdot(a-bQ)-(c+t)\cdot Q=-bQ^2+(a-c-t)\cdot Q \textbf{ (2 балла)}\)
Это парабола ветвями вниз относительно Q, прибыль максимальна в вершине (1 балл за обоснование, 1 балл за правильные выпуск и цену):
\(Q^*=\dfrac{a-c-t}{2b}; \quad P^*=\dfrac{a+c+t}{2}\)
В условиях нашей задачи $a-c=3 \gt 0$, значит, до введения налога оптимум не в нуле:
\(\begin{array}{l} CS=\dfrac{a-P}{2}\cdot Q=\dfrac{a-c-t}{4}\cdot Q \\ \pi = TR-TC=\dfrac{a-c-t}{2}\cdot Q \\ T=t\cdot Q\end{array}\)
Тогда:
\(\begin{array}{l} SW=CS+\pi +T \\ SW=\dfrac{Q}{4}\cdot (3(a-c)+t)=\dfrac{1}{4}\cdot \left(-t^2-2(a-c)t+3(a-c)^2\right) \end{array}\)
(По 1 баллу за каждое выражение и за суммарную функцию. Всего 4 балла. Если слагаемые не были выписаны ранее, но функция верная, то за суммарную функцию всё равно ставить 4 балла)
Это парабола ветвями вниз относительно $t$. Оптимум в вершине, $t^*=c-a=-3$, то есть необходимо ввести субсидию в размере 3 у.е. (1 балл за обоснование, 2 за ответ).
2. Немного про Джини
В случае, когда есть две однородные группы, кривая Лоренца выглядит так:
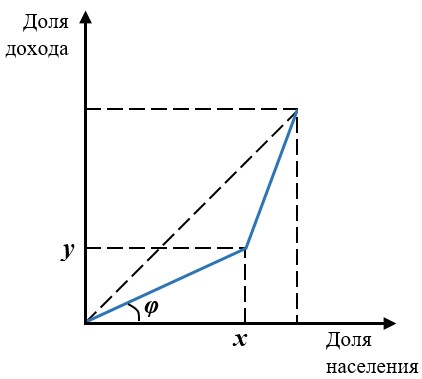
Сначала поясним, как найти индекс Джини, зная долю доходов бедных и долю их численности.
Площадь под кривой Лоренца равна:
\[\dfrac{1}{2}xy+\dfrac{y+1}{2}\cdot (1-x)=\dfrac{1}{2}(y-x+1)\]
Площадь между кривой равномерного распределения доходов и кривой Лоренца:
\[\dfrac{1}{2}-\dfrac{1}{2}(y-x+1)=\dfrac{1}{2}(x-y)\]
Таким образом, индекс Джини равен: $G=\dfrac{\dfrac{1}{2}(x-y)}{\dfrac{1}{2}}=x-y$
$G=x-y$, где $x$ – доля бедных (в этом случае доля аналитиков), а $y$ – это доля фонда оплаты труда, приходящаяся на аналитиков (4 балла за соотношение). Фирму «Равенство и Братство» обозначим индексом 1, а «Рога и Копыта» – индексом 2. Можем записать следующие уравнения:
\[\begin{array}{l} 1-y_2=1{,}5\cdot(1-y_1) \\ y_2=1{,}5y_1-0{,}5 \quad \textbf{(3 балла)}\end{array}\]
Также известно, что $G_1=x-y_1, G_2=x-y_2$
Решая, получаем, что $x=3G_1-2G_2+1=3\cdot0{,}3-2\cdot0{,}5+1=0{,}9 \quad \textbf{(4 балла)}$
3. Рыночное предложение
- Фирмы типа А в количестве 100 штук, каждая с функцией общих издержек $TC(A)=q^2+3q+300$
- Фирмы типа Б в количестве 50 штук, каждая с функцией общих издержек $TC(Б)=0{,}5q^2+4q+270$.
Выведите функцию рыночного предложения данной отрасли для краткосрочного периода.
\[\begin{equation}P\lt \min AVC \rightarrow P \lt AVC \rightarrow P\cdot q \lt AVC\cdot q \rightarrow TR \lt VC \rightarrow TR-VC \lt 0 \rightarrow \\ (TR-VC-FC)+FC\lt 0 \rightarrow PR+FC\lt0 \rightarrow PR\lt -FC\end{equation}\]
В этом случае фирме невыгодно выходить на рынок.
Таким образом, для фирмы каждого типа функция предложения будет иметь вид:
\[q(s)=\begin{cases}0, &\text{при } 0 \leq P \lt\min AVC \\ q(P), & \text{при } P\geq \min AVC \qquad \textbf{(1 балл)}\end{cases}\]
Исходя из этих условий, выведем теперь функцию предложения для одной фирмы каждого типа.
Для фирм типа А $AVC(q)=\dfrac{VC(q)}{q}=\dfrac{q^2+3q}{q}=q+3$. Минимум этой функции достигается при $q=0 \rightarrow \min AVC=3$.
Значит, при $P\lt3$ для фирмы типа А $q=0$. При $P \geq 3$ для максимизации прибыли фирма будет выбирать количество по принципу $P=MC(q)$.
Для фирм типа A $MC(q)=TC'(q)=2q+3$.
Тогда $P=2q+3 \rightarrow q=0{,}5P-1{,}5$.
Таким образом, предложение фирмы типа А имеет вид:
\[q(s)=\begin{cases}0, &\text{при } 0 \leq P \lt3 \\ 0{,}5P-1{,}5, & \text{при } P\geq 3 \qquad \textbf{(2 балла)}\end{cases}\]
и так как фирм типа А на данном рынке действует 100, то их совокупное предложение будет иметь вид: \(Q(s)=\begin{cases}0, &\text{при } 0 \leq P \lt3 \\ 50P-150, & \text{при } P\geq 3 \end{cases} \quad \textbf{(2 балла)}\).
Аналогично, для фирм типа Б $AVC(q)=\dfrac{VC(q)}{q}=\dfrac{0{,}5q^2+4q}{q}=0{,}5q+4$. Минимум этой функции достигается при $q=0 \rightarrow \min AVC=4$.
Значит, при $P\lt4$ для фирмы типа Б $q=0$. При $P \geq 4$ для максимизации прибыли фирма будет выбирать количество по принципу $P=MC(q)$.
Для фирм типа Б $MC(q)=TC'(q)=q+4$.
Тогда $P=q+4 \rightarrow q=P-4$.
Таким образом, предложение фирмы типа Б имеет вид:
\[q(s)=\begin{cases}0, &\text{при } 0 \leq P \lt4 \\ P-4, & \text{при } P\geq 4 \qquad \textbf{(2 балла)}\end{cases}\]
и так как фирм типа Б на данном рынке действует 50, то их совокупное предложение будет иметь вид: \(Q(s)=\begin{cases}0, &\text{при } 0 \leq P \lt4 \\ 50P-200, & \text{при } P\geq 4 \end{cases} \quad \textbf{(2 балла)}\).
Совокупное предложение на рынке найдём путём суммирования по горизонтали индивидуальных кривых предложения двух типов фирм (двух групп производителей):
\[Q(s)=\begin{cases}0, & \text{при } 0 \leq P \lt 3 \\ 50P-150, & \text{при } 3 \leq P \lt 4 \\ 100P-350, & \text{при } P \geq 4 \end{cases} \quad \textbf{(2 балла)}\]
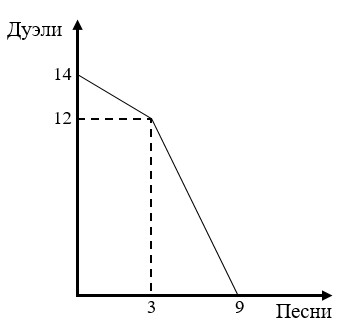
4. Рэперская

Оценим альтернативные издержки подготовки единицы концерта каждым из рэперов:
\[\begin{array}{l} X: OC(1K)=2(A) \\ Y: OC(1K)=\dfrac{2}{3}(A) \\ \textbf{(1 балл за построение КПВ и вычисление альтернативных издержек)}\end{array}\]
Заметим, что для организации деятельности им необходимо использовать общий ресурс – арендованную студию, поэтому «объединять» их производственные возможности недопустимо (2 балла за данную мысль)
Очевидно, что при эффективном разделении труда MC Икс должен записывать альбомы, а МС Игрек – проводить концерты, так как альтернативные издержки проведения концертов ниже у МС Игрека (или с учётом его производственных возможностей) (1 балл за сравнение альтернативных издержек и определение специализации).
Тогда максимальное количество концертов, которое может быть организовано ими совместно, совпадает с максимальным количеством концертов МС Игрека (15), если студией весь год будет пользоваться Игрек. А максимальное количество альбомов – с максимальным количеством альбомов МС Икса (20), если студией весь год будет пользоваться Игрек (1 балл за определение максимальных объемов производства благ).
Поскольку оборудование на студии может использоваться как одним из них, так и другим, рассмотрим вариант деления оборудования.
Пусть $t$ – часть года, в течение которого МС Икс использует студию. Тогда за это время он сможет выпустить $20t$ альбомов.
Тогда МС Игрек будет использовать студию $(1–t)$ часть года и сможет провести $15(1–t)$ концертов (1 балл).
Имеем систему:
\[\begin{cases} A=20t \\ K=15(1-t) \\ 0\leq t \leq 1 \end{cases} \quad \textbf{(3 балла за составление системы)}\]
Выразим $t$ из первого уравнения и подставим его во второе:
\[\begin{cases} t=\dfrac{1}{20}A \\ K=15-\dfrac{3}{4}A \\ 0\leq A \leq 20 \end{cases} \quad \textbf{(2 балла за решение системы и ответ)}\]