1. Что делать, если график MC напоминает горный пейзаж?
В связи с внедрением сложной системы субсидирования график предельных издержек совершенно конкурентной фирмы имеет несколько нетипичный вид:
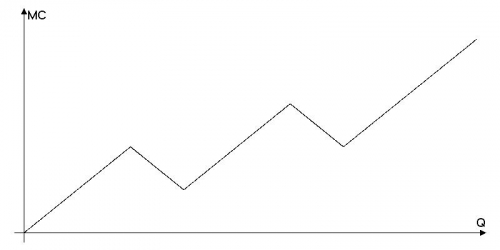
Постройте на этом же графике кривую предложения фирмы и подробно объясните свое решение.
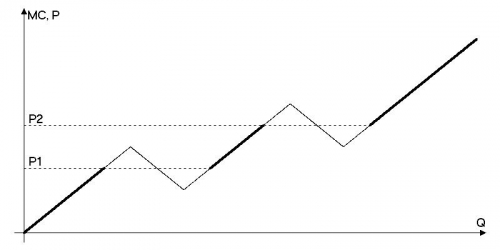
Если уравнение $MC(Q) = P$ имеет один корень, кривая предложения совпадает с кривой $MC$.
Если корней несколько, то нужно выбрать тот выпуск, при котором прибыль будет больше. Во-первых, заметим, что мы никогда не выберем точку на убывающем участке $MC$, так как это точка локального минимума функции прибыли. Значит, мы всегда будем выбирать только корень уравнения $MC(Q) = P$, лежащий на возрастающем участке графика $MC$.
На следующем этапе для определения оптимального выпуска необходимо сравнить величины прибыли, которую фирма получит, выбирая больший или меньший объемы выпуска, соответствующие возрастающим участкам графика $MC$. Для этого удобно использовать площади треугольников, заключенных между графиками $P$ (для какого-то $P$) и $MC$. Площадь «верхнего» треугольника при каком-то $P$ равна дополнительным убыткам перехода от меньшего выпуска к большему, а «нижнего» - дополнительным выгодам. Тогда если больше площадь «нижнего» - то есть дополнительные выгоды больше дополнительных убытков – то кривой предложения будет принадлежать больший выпуск. Если же больше площадь «верхнего» треугольника – то есть дополнительные убытки больше дополнительных выгод – то выгоднее будет производить меньший объем выпуска.
Если площади указанных треугольников равны (как при ценах$P_1$ и $P_2$) – возникает точка разрыва функции предложения; фирме безразлично, какой из двух объемов выбрать (при этом обе интересующие нас точки включаются в график кривой предложения).
Поскольку указанные треугольники подобны, $P_1$ лежит ровно посередине между соответствующими локальным максимумом и минимумом $MC$. Аналогично для $P_2$.
2. Железо, дерево и глина
В античном городе N в производстве различных товаров используются три вида ресурсов: Железо (A), Дерево (B) и Глина (C). Кривая, описывающая возможности города в добыче ресурсов, задается уравнением $A^2+B^2+C^2=90000$. Все производимые в городе товары можно разделить на две группы: Военные Товары (X) и Мирные Товары (Y). В среднем для производства единицы Мирных Товаров необходимы 1 единица Железа, 2 единицы Дерева и 2 единицы Глины. Для производства единицы Военных Товаров нужно 4 единицы Железа и 3 единицы Дерева, Глины не нужно вовсе.
Война с античным городом М не за горами, поэтому необходимо точно оценить потенциал города в производстве Военной и Мирной продукции. Выведите уравнение кривой производственных возможностей города N в координатах (X,Y) и постройте её график, указав максимально возможные объемы производства военных и мирных товаров.
Для производства Х единиц Военной и Y единиц Мирной продукции нужно $A = 4X + Y$единиц Железа, $B = 3X + 2Y$ единиц Дерева, $C = 2Y$ единиц Глины. Подставляя эти выражения в КПВ ресурсов, получаем:
$(4X + Y)^2 + (3X + 2Y)^2 + (2Y)^2 = 90000 $ или $25X^2 + 20XY + 9Y^2 = 90000$.
Это и есть искомое уравнение КПВ. Решив это уравнение относительно Y, можно получить явную зависимость Y(X): $Y = {{\sqrt {810000 - 125X^2 } - 10X} \over 9}$ (хотя делать это, в принципе, не обязательно).
КПВ будет иметь обычный вогнутый вид, max(X) = 60, max(Y) = 100.

Ответ: Уравнение кривой, описывающей возможности города в производстве военной и мирной продукции:$Y = {{\sqrt {810000 - 125X^2 } - 10X} \over 9}$. Максимально возможный объем производства военных товаров равен 60, мирных товаров – 100.
3. 1000 спросов
На рынке присутствуют 1000 покупателей, для удобства дальнейших рассуждений пронумерованных индексами $i=1,\ 2,\ 3,\ \dots,\ 1000$. Функция спроса i-го покупателя имеет вид: $q_i=1001-i-P$. Причем цены могут принимать только целые значения. Производит и продает товар фирма-монополист, функция общих издержек которой имеет вид $TC=100,5Q$. Сколько единиц товара и по какой цене продаст монополист, не имеющий возможности осуществлять ценовую дискриминацию? Какую прибыль он получит?
Очевидно, график функции спроса каждого отдельного покупателя будет представлять тобой отрезок прямой. Поскольку индивидуальные графики спроса начинаются при различных максимальных значениях цены, то суммарная (рыночная) функция спроса будет иметь график, представляющий собой ломаную линию. Представим точки перелома этой линии в виде таблицы, формулирующей зависимость между ценой и объемом товара, приобретенного всеми покупателями:
| P | 1000 | 999 | 998 | 997 | … | P |
| Q | 0 | 1 | 1+2 | 1+2+3 | 1+2+3+…+1000-P |
Используя формулу суммы членов арифметической прогрессии, можно записать:
$Q(P)=1+2+3+\dots+(1000-P)=\\= {{1 + (1000 - P)} \over 2} \cdot (1000 - P)=0,5(1001-P)(1000-P) $
Разумеется, это уже не график ломаной линии. Это парабола, которая при целых значениях Р и Q проходит через точки ломаной линии спроса. Однако, именно при целых значениях данная зависимость нас и интересует. Графически полученный результат можно представить следующим образом:
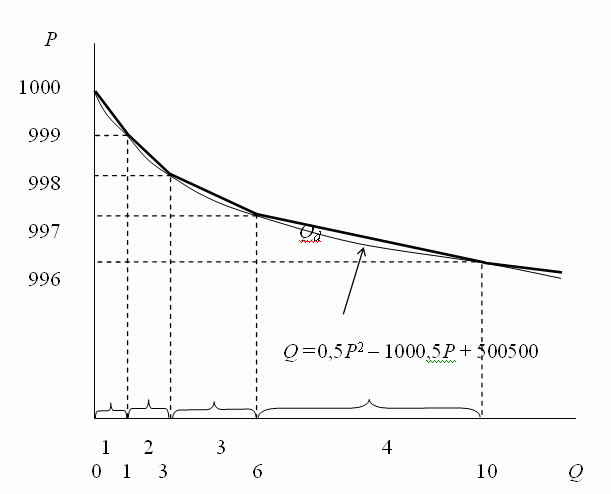
Запишем выражение для прибыли монополиста при определенном значении Р:
$\pi =TR-TC=P\cdot Q(P)-100,5\cdot Q(P)=\\=(P-100,5) \cdot 0,5(P-1001)(P-1000)$
График этой функции – кубическая парабола, проходящая через точки 100,5; 1000; 1001.
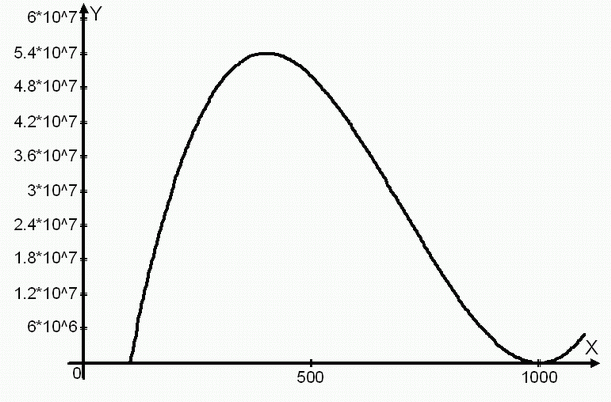
Спрос определен при $Q \le 1000 $. На участке (100,5;1000) эта функция имеет максимум. Найдем P такое, что $\pi(P)=\pi(P-1) $. Если это P целое, то P и P-1 – точки с максимальной прибылью среди всех целых P. Если это P не целое, то максимальную прибыль обеспечит целое число, лежащее между (P-1) и P.
Значит, P=401 и P=400 являются решениями задачи.
4. Евро за килограмм
- 0 < Q < 30; 21>t>12; 22-0,2Q=1+0,1Q+t; Q=70-3,33t
- 30 < Q < 66,67; 12>t>17/6; 22-0,2Q=2,5+0,05Q+t; Q=78-4t
- 66,67 < Q < 95; 17/6>t>0; 12-0,05Q=2,5+0,05Q+t; Q=95-10t
5. Спрос касается AC
На рисунке представлены графики предельных (MC) и средних (АС) издержек фирмы-монополиста. А также график спроса на его продукцию (D).
Определите, какой объем выпуска должна выбрать фирма, чтобы максимизировать прибыль (минимизировать убытки)? Восстановите уравнение кривой спроса.
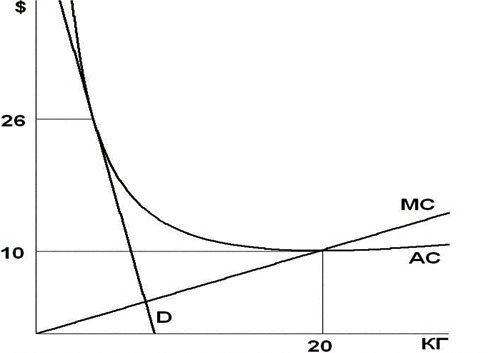
Функция предельных издержек проходит через точки $(0;0)$ и $(20;10)$, следовательно, предельные издержки заданы уравнением: $MC(Q)=0,5Q$. Значит, уравнение общих издержек имеет вид: $TC(Q)=0,25Q^2+FC$. Отсюда $FC=100$. Функция средних издержек задается уравнением: $AC(Q) = \frac{TC(Q)}{Q} = 0,25Q + \frac{100}{Q}$.
Из графика видно, что при объеме, соответствующем $P=26$, средние издержки равны 26 долларам и следовательно прибыль монополиста равна нулю. При любом другом объеме график спроса лежит ниже графика средних издержек, следовательно, прибыль монополиста отрицательна. Поэтому максимальная (нулевая) прибыль монополиста достигается при цене, равной 26. Значит, оптимальный объем выпуска, как следует из графика, является наименьшим из корней уравнения: $AC(Q) =26$. $0.25Q + \frac{100} {Q} = 26 \Leftrightarrow Q^2 - 104Q + 400 = 0 \Leftrightarrow Q=4 \ \ \ Q=100.$ Нас устраивает наименьший из корней: $\fbox{Q*=4}$.
Нам известна одна точка на кривой спроса: $Q=4 \ ; P=26.$ Так что $MC(4) = 2; \ MR(4) = 2 \ ; \ Q_d(2) = 8$ (кривая спроса вдвое положе кривой $MR(Q)$). Таким образом, нам известна вторая точка на кривой спроса: $ Q=8 ;\ P=2$ и уравнение кривой спроса: $\fbox{P = 50 - 6Q}$