Если число участников схемы конечно, то система является замкнутой и сумма денег в ней фиксирована. Значит, если хотя бы у одного человека получится выиграть, то найдется хотя бы один человек, который проиграет. Поэтому всем заработать с помощью такой схемы не получится. Это, однако, не означает, что никому не удастся заработать. Возможность получения прибыли участниками схемы зависит от того, насколько рационально ведут себя люди.

Рассмотрим сначала ситуацию, в которой все люди ведут себя рационально. Допустим, что каждый человек может поучаствовать в схеме не более одного раза. Так как по нашему предположению число участников схемы конечно, то в некоторый момент обязательно останутся те, кто на последнем этапе получили письмо, но не могут переслать его другим людям, не являющимся участниками схемы. Такие люди откажутся участвовать в заведомо убыточной для них схеме, так как они должны заплатить отправителю письма, но не могут ничего получить взамен. Далее, участники схемы, которые посылают письма на предпоследнем этапе, также не получат никаких доходов, так как те, кому они послали письма, откажутся участвовать в этом. Но тогда уже участникам предпоследнего этапа не выгодно участвовать в схеме, и так далее. Следуя по данной цепочке рассуждений к самому началу схемы, мы убедимся, что те, кому М. отправил первые письма, откажутся принимать участие в этом начинании. Таким образом, идея предпринимателя М. работать не будет ему никто не заплатит.

Подобные схемы называются пирамидами. На практике большое количество людей оказывается вовлеченными в такие схемы. Это происходит из-за того, что люди не всегда ведут себя рационально. Во-первых, люди, не понимая механизма пирамиды, могут принять ошибочное решение об участии в ней. Во-вторых, даже если люди понимают этот механизм, они надеются оказаться умнее других и заработать за счет других, менее рациональных с их точки зрения участников. Иными словами, они рассчитывают, что не окажутся в числе последних желающих участвовать в пирамиде. А все, кроме самых последних участников пирамиды, действительно зарабатывают!

Отметим важную роль предположения о конечности участников схемы и аналогичного по смыслу предположения о том, что каждый участник может участвовать в схеме не более одного раза. Если «пирамида» растянута во времени, то число ее участников, вообще говоря, может быть неограниченным. Так работают многие государственные пенсионные системы, когда человек на протяжении своей трудовой деятельности отдает некоторую долю своего заработка в распоряжение пенсионного фонда и тем самым финансирует нынешних пенсионеров, а после выхода на пенсию получает пенсию за счет отчислений работающих людей.

Предложенный изначально способ дает ошибку, поскольку он не учитывает долю занятых лиц в регионе относительно общего количества занятых в стране. В качестве простого примера рассмотрим страну, в которой есть всего два региона. В одном из них число занятых равно 100 человек, а во втором 20. Если в первом регионе средняя зарплата равна 10, а во втором 20, то первый предложенный метод оценит среднюю зарплату по всей стране так:
$$
\frac{10+20}{2}=15.
$$
Однако это не соответствует действительности. По определению, средняя зарплата по всей стране это суммарная оплата труда, деленная на общее число занятых. Поэтому в данном примере средняя зарплата равна
$$ \frac{100\times 10+20\times 20}{100+20}=\frac{1400}{120}=\frac{35}{3}.
$$

Рассмотрим общий случай. Обозначим за $k$ число регионов в России. У исследователя имеются данные о численности занятого населения в каждом регионе $N_i$, $i=1,2,\ldots,k$, а также данные по средним зарплатам в каждом регионе $W_i$, $i=1,2,\ldots,k$. Тогда суммарная зарплата в $i$-м регионе равна $W_i\times N_i$, $i=1,2,\ldots,k$, а суммарная зарплата по всей России равна $W_1\times N_1+W_2\times N_2+\times+W_k\times N_k$. Общее число занятых лиц в России равно $N_1+N_2+\ldots+N_k$. Следовательно, средняя зарплата в России может быть вычислена как
$$
\frac{W_1\times N_1+W_2\times N_2+\ldots+W_k\times N_k}{N_1+N_2+\ldots+N_k}.
$$

Во всех описанных случаях люди (правительства) предпринимают затратные действия, чтобы ограничить множество своих возможных действий в будущем. При некоторых вариантах развития событий у них могжет возникнуть соблазн отклониться от своих долгосрочных планов. Они могут решить ретироваться на кораблях, перестать ходить в фитнес-клуб или резко увеличить вредное для окружающей среды производство. Если же заранее лишить себя возможности так поступить, можно достичь более выгодного результата. Солдаты, зная, что отступать некуда, будут лучше драться; человек, купивший абонемент, скорее пойдет в фитнес-центр, так как деньги он уже потратил, и так далее.

а)Объяснение этого эффекта кроется в том, что люди дисконтируют свое будущее благосостояние: с точки зрения сегодняшнего дня получение зарплаты сейчас принесет б'ольшую полезность, чем получение такой же зарплаты через неделю; съесть шоколадку сегодня приятнее, чем съесть такую же шоколадку завтра; уплатить штраф за нарушение правил дорожного движения сегодня неприятнее, чем завтра. Это происходит из-за фактора неопределенности (до следующего периода может что-нибудь случиться), из-за упущенной выгоды (деньги, полученные сегодня, можно положить на депозит и получить в следующем периоде проценты) и просто из-за того, что люди нетерпеливы. Для людей предпенсионного возраста повышение возраста выхода на пенсию затрагивает их самое ближайшее будущее, в то время как на молодежи это изменение может отразиться лишь в долгосрочной перспективе (оно сократит количество шоколадок, которые они смогут съесть через 30 лет, но из-за дисконтирования они сейчас придают маленькое значение удовольствию от этих шоколадок). Поэтому при одинаковых взглядах на проблему повышения пенсионного возраста пожилые люди будут проявлять гораздо большее недовольство, чем молодежь.
б) Преимущество данной схемы заключается в том, что для людей, которым предстоит выход на пенсию в ближайшем будущем, этот переход будет меньшим шоком, чем одномоментное резкое повышение пенсионного возраста. У людей появится возможность лучше подготовиться к нескольким лишним годам работы и пересмотреть свои финансовые стратегии. Для правительства это означает меньшие политические риски. Недостаток заключается в том, что если существует текущий дефицит бюджета пенсионного фонда, то предложенный метод не позволит решить проблему быстро или даже в течение нескольких лет. В долгосрочном периоде, когда реформа завершится через 10 лет, система будет более сбалансированной. Однако до этого, на протяжении этих лет, необходимо будет изыскать источник покрытия сложившегося дефицита.

С одной стороны, рост цен на перевозку грузов железнодорожным транспортом может быть вызван ростом цен на электроэнергию. Из-за более дорогого электричества увеличиваются издержки на транспортировку грузов с помощью электровозов, а рост цен на перевозку с помощью тепловозов может быть следствием роста цен на взаимозаменяемый товар. С другой стороны, необходимо помнить, что после этого не значит из-за этого. Очевидно, что электроэнергия не единственный источник расходов железнодорожных компаний. Так, рост цен на электроэнергию может быть вызван ростом цен на уголь основное топливо ТЭЦ и ГРЭС. Таким образом, рост цен на уголь мог спровоцировать и рост цен на перевозки грузов тепловозами, и рост цен на электроэнергию, что, в свою очередь, повлекло рост цен на перевозки грузов электровозами. Успех политики сдерживания роста цен на перевозки с помощью ограничения цен на электроэнергию зависит от настоящей причины роста цен на перевозку товаров. Если имел место рост цен на уголь, то ограничение цен на электроэнергию не отразится на ценах на железнодорожные перевозки с помощью тепловозов, и, соответственно, эффект роста цены взаимозаменяемого товара будет толкать цены на перевозки с помощью электровозов вверх. В такой ситуации влияние этой меры на конечные тарифы перевозок будет незначительным. Однако если рост цен на перевозки действительно был вызван
ростом цен на электроэнергию, то предложенная политика будет эффективной.

Разные потребители по-разному оценивают офисные программы: кому-то больше нужен текстовый процессор, кто-то чаще пользуется редактором электронных таблиц, а для кого-то главная функция создание презентаций. Соответственно отличаются и денежные суммы, которые они готовы платить за каждый продукт. Если продавать программы по отдельности, то на каждую из них придется назначать единую цену, и если эта она будет высокой, то те потребители, которые ценят данную программу меньше, не купят ее. Если же эта цена будет низкой, то программу купят больше потребителей, но самые платежеспособные из них заплатят существенно меньше, чем могли бы.

Однако общая сумма, которую готовы заплатить за комплект программ потребители из той или иной группы, вполне может быть примерно одинаковой, и тогда назначение цены пакета в виде этой общей суммы позволит продать товар всем и в то же время заставит всех платить примерно столько, сколько они готовы. Чтобы лучше понять эту логику, рассмотрим следующий пример. Пусть есть два потребителя, каждый из которых предъявляет спрос на две программы: текстовый процессор и редактор презентаций. Суммы, которые каждый из них готов заплатить за программы и за их набор, представлены в таблице:

	Потребитель А	Потребитель Б
Текстовый процессор	100	70
Редактор презентаций	70	100
Набор	170	170

Если бы производитель назначал цену на каждый продукт в отдельности и максимизировал выручку (Максимизация выручки резонная предпосылка, так как издержки производителей программного обеспечения практически не зависят от количества проданных копий)., то он бы назначил цену 70 на обе программы, оба потребителя бы купили и текстовый процессор, и редактор презентаций, выручка при этом равнялась бы 280 д. е. Если же продавать программы в наборах по цене 170 д. е. за набор, то оба потребителя купят набор и выручка составит 340 д. е.

Кроме того, производитель понимает, что существует несколько групп потребителей, представители которых существенно отличаются платежеспособностью (например, крупные компании готовы заплатить существенно больше, чем студенты, использующие компьютер дома). Чтобы максимизировать доход, производителю было бы выгодно продавать набор программ представителям каждой группы именно за такую сумму, которую каждый из них готов заплатить, но добиться этого непросто: крупные компании стали бы отправлять за покупками студентов, если бы для тех была существенная скидка. Решение заключается в осознании того, что представителям разных групп нужны разные наборы программ: например, если кто-то предъявляет спрос на средство управления базами данных или менеджер проектов, то он, скорее всего, делает покупку для компании. Поэтому можно продавать несколько видов наборов, каждый для своей группы потребителей. Например, набор для домашнего использования может включать только основные программы и стоить дешевле, тогда как пакет, состоящий в том числе из профессиональных программ существенно дороже. Домашние пользователи не будут покупать профессиональный пакет, так как он для них очень дорог и включает не очень нужные программы, а крупные компании не будут покупать домашний пакет, так как в нем нет необходимых для них программ. Таким образом, потребители из более платежеспособной группы будут платить больше, чем потребители из менее платежеспособной группы.

Заметим также, что продажа офисных программ в наборах может быть дешевле отдельной продажи: не нужно записывать несколько дисков (если программы продаются на дисках), упаковывать их в несколько коробок и т. п. К тому же, покупатели и без объединения в наборы покупали бы несколько программ одного производителя: они лучше совместимы между собой.

n Обычно люди ценят последующие единицы продукта меньше, чем первую. В частности, потребители готовы заплатить б'ольшую сумму за то, чтобы офисные приложения были установлены хотя бы на одном из их домашних компьютеров (на том, где они необходимы больше всего), чем за то, чтобы они появились еще и на ноутбуке восьмилетней дочки. Продажа товаров наборами позволяет делать так, чтобы за покупку следующих единиц потребители платили меньше, чем за первую: в описанном в задаче примере вторая и третья копия программного пакета стоят (вместе!) всего лишь 35 % стоимости первой. Таким образом достигается та же цель, что и в пункте а): те единицы товара, которые ценятся потребителями меньше, продаются дешевле.

Многие американцы любят после окончания рабочего дня или окончания рабочей недели провести время в баре или ресторане с друзьями. Нередко такой досуг сопровождается потреблением алкоголя и курением. Введение запрета на курение в барах и ресторанах создает неудобство тем, кто любит сопровождать распитие спиртных напитков курением. С введением запрета такие люди вынуждены идти на ухищрения. Они должны или найти бары и рестораны, которые не соблюдают новый закон, или выехать за пределы административного образования, которое запрещает курение в барах и ресторанах. В обоих случаях это приводит к тому, что те, кто хочет выпить и покурить одновременно, вынуждены вести машину на более длинную дистанцию после запрета, чем до запрета. При возвращении домой пьяные посетители ресторанов и баров управляют машиной дольше, чем до запрета. Следовательно, повышается вероятность ДТП.

а) Если Костя отдаст Жене один талон на колу, а взамен получит один талон на жвачку, то они оба выиграют от такого обмена, так как по условию оба мальчика ценят разнообразие. Они по-прежнему будут потреблять две единицы продукта в день, но это будут разные продукты (кола и жвачка, а не только что-то одно). Очевидно, что это взаимовыгодный обмен.

Отметим, что обмен двух талонов на колу на два талона на жвачку также может быть взаимовыгодным при некоторых предпочтениях ребят. Действительно, если предпочтения ребят устроены так, что для Кости две жвачки лучше, чем две колы, а для Жени наоборот, то оба мальчика выиграют, если поменяются всеми талонами.

б) Допустим, мальчики решили организовать взаимовыгодный обмен. Пусть сначала Женя отдает свой талон на жвачку Косте, а потом Костя решает, отдавать ли свой талон на колу Жене. В этом случае Косте не выгодно отдавать Жене свой талон на колу, так как для Кости одна жвачка и две колы что лучше, чем одна жвачка и одна кола. Женя не может потребовать свой талон обратно, поэтому он изначально не согласится на такую процедуру обмена. А Костя изначально согласен на последовательный обмен, но после того, как он получит талон на жвачку от Жени, он нарушит свое обещание и не отдаст Жене свой талон на колу. Обмен не состоится.

в) Отличие этой ситуации от предыдущего пункта в том, что возможность повторного взаимовыгодного обмена ограничивает стимулы Кости сжульничать. Если Костя обманет Женю уже в первый день, то Женя может не согласиться совершать взаимовыгодные обмены в будущем, что невыгодно для Кости. В первый день Костя готов отдать свой талон на колу, чтобы взаимовыгодный обмен состоялся и чтобы Женя был готов совершить обмен на следующий день. Иными словами, Костя готов создать репутацию ради дальнейшей пользы. Однако в самый последний день недели (года), Косте не нужно будет поддерживать свою репутацию и, если Женя согласится на обмен, то Костя не отдаст ему свой талон на колу. Зная это, Женя не согласится на обмен в последний день недели (года), то есть обмен в последний день не состоится. Теперь предпоследний день недели (года), в течение которой (которого) мальчики договорились меняться, станет последним. Однако, следуя той же логике, Костя не отдаст Жене свой талон, если Женя согласится на обмен. Предвидя это, Женя на обмен не согласится, и в предпоследний день недели (года) обмен также не состоится, и так далее. Таким образом, обмен не состоится и в самый первый день, Женя на такую процедуру не согласен.

Последовательные стратегические взаимодействия нескольких лиц удобно анализировать «с конца», как это было сделано в этой задаче, а также в задаче 1. Это называется методом обратной индукции.

а) Пусть $O$ точка пересечения диагоналей четырехугольника $ABCD$, а $O_1$ произвольная точка плоскости, отличная от точки $O$. Докажем, что $O_1A+O_1B+O_1C+O_1D > OA+OB+OC+OD$. Если $O_1$ не лежит на прямых $AC$ или $BD$, то, по неравенству треугольника, $O_1A+O_1C > AC=OA+OC$, $O_1B+O_1D > BD=O_1B+O_1D$. Сложив почленно эти два неравенства, получим, что $O_1A+O_1B+O_1C+O_1D > OA+OB+OC+OD$. Остается рассмотреть случай, когда $O_1$ лежит на одной из прямых $AC$ или $BD$. Пусть $O_1$ лежит на прямой $AC$. Тогда снова, в силу неравенства треугольника, $O_1B+O_1D > BD=O_1B+O_1D$. Так как точки $A,O_1,C$ лежат на одной прямой, то к ним применить неравенство треугольника нельзя. Тем не менее, очевидно, что в этом случае справеливо более слабое неравенство $O_1A+O_1C \geqslant AC=OA+OC$. Сложив почленно два неравенства, снова получим, что $O_1A+O_1B+O_1C+O_1D > OA+OB+OC+OD$. Случай, когда точка $O_1$ лежит на прямой $BD$, рассматривается аналогично. Таким образом, сумма расстояний до всех четырех городов от точки $O$ меньше, чем от точки $O_1$. Значит, $O$ общественно оптимальная точка и других общественно оптимальных точек нет.

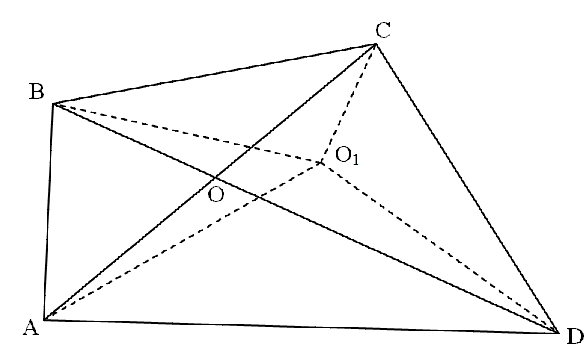
б) Назовем точку, которую не побеждает никакая другая точка, непобедимой. Докажем, что (i) точка пересечения диагоналей является непобедимой; (ii) никакая другая точка непобедимой не является.

(i) Проведем через точку пересечения диагоналей прямые, перпендикулярные им. Эти прямые разобьют плоскость на 4 области, обозначенные за I, II, III, IV. Допустим, на голосование против точки $O$ выносится точка $X$. Окружность с центром в вершине четырехугольника, проходящая через точку O, будет касаться одного из перпендикуляров. Поэтому если точка $X$ принадлежит области I, то за $O$ (и против $X$) будут голосовать как минимум города $A$ и $B$; если точка $X$ принадлежит области II, то за $O$ будут голосовать как минимум города $A$ и $D$; если $X$ принадлежит области III, то за $O$ будут голосовать как минимум города $D$ и $C$, а если $X$ принадлежит области IV, то за $O$ будут голосовать как минимум города $B$ и $С$. Наконец, если точка $X$ лежит на одном из перпендикуляров, то как минимум три города будут голосовать за $O$. Таким образом, точка $O$ действительно непобедимая.

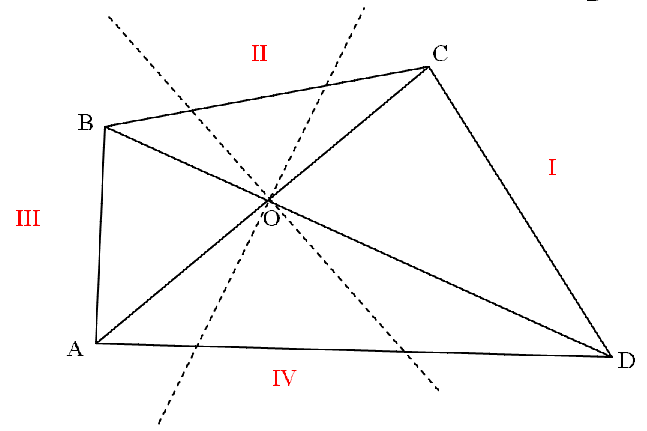
(ii) Теперь докажем, что любую другую точку можно победить.
Возьмем произвольную точку $X$, не совпадающую с $O$. Опустим из нее перпендикуляр на какую-нибудь диагональ (это всегда можно сделать, ведь $X$ не лежит хотя бы на одной из диагоналей). Обозначим эту диагональ за $d$, а полученную точку за $Y$. Докажем, что точка $Y$ побеждает точку $X$. Заметим, что если на голосование будут вынесены $Y$ и $X$, то города, расположенные в концах диагонали $d$, будут голосовать за Y (перпендикуляр является кратчайшим расстоянием от точки до прямой). Кроме того, за $Y$ обязательно будет голосовать город, расположенный относительно точки $X$ по другую сторону от диагонали $d$. Почему это так? Обозначим этот город за $G$. Заметим, что $\triangle GYX$ тупоугольный, в нем $\angle GYX>90^{circ}$ по построению. Отсюда следует, что сторона $GX$ в нем самая большая. Следовательно, $GX>GY$, и город $G$ будет голосовать за $Y$. Итак, мы нашли три города, которые будут голосовать за $Y$. Значит, точка $X$ не является непобедимой.

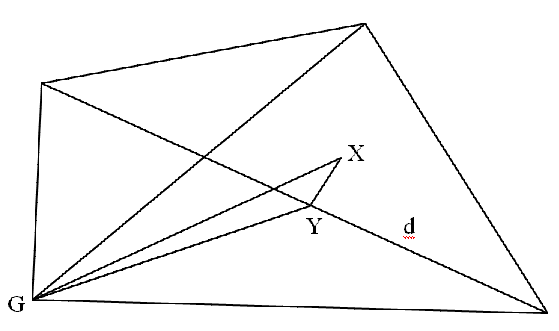
Вывод: множество непобедимых точек состоит из одной точки точки пересечения диагоналей. Она, как было показано ранее, является и общественно оптимальной.

Дополнительные задания:

item Придумайте свою «негеографическую» интерпретацию задачи (подсказка: представьте, что есть компания из четырех экономических агентов, которая решает, на каком уровне установить значения неких двух переменных, влияющих на благосостояние каждого из них четырех).
item Обобщите результаты для выпуклого $n$-угольника, $n \geqslant 3$. При каких $n$ множество непобедимых точек в общем случае непусто (включает хотя бы одну точку)? При каких $n$ какая-нибудь из непобедимых точек будет еще и общественно оптимальной?

a) Поскольку иметь на руках доллары или евро в конце дня запрещено, существует только два способа получить доход: «крутить» деньги в течение одного дня между валютами, зарабатывая на разнице курсов (получение такого безрискового дохода называется арбитражем), или класть деньги в банк под проценты, причем из-за условий задачи в банк можно класть только фантики. Так как $33 \times 1{,}28=42{,}24 < 43$, то в понедельник самой выгодной из арбитражных схем является схема «фантики $\rightarrow$ доллары $\rightarrow$ евро $\rightarrow$ фантики»; так как $32{,}9 \times 1{,}36=44{,}744 > 43{,}4$ и $33{,}6 \times 1{,}3=43{,}68 > 43{,}1$, то во вторник и среду самой выгодной из арбитражных схем является схема «фантики $\rightarrow$ евро $\rightarrow$ доллары $\rightarrow$ фантики». Рассмотрим доходность по каждой из двух операций в каждый из трех дней, они приведены в таблице ниже.

	Процент с депозита	Валютный арбитраж
Понедельник	2 %	$((100:33):1{,}28) \times 43 \approx 101{,}8 \Rightarrow 1{,}8 %$
Вторник	2 %	$((100:43{,}4) \times 1{,}36) \times 32{,}9 \approx 103{,}1 \Rightarrow 3{,}1 %$
Среда	2 %	$((100:43{,}1) \times 1{,}3) \times 33{,}6 \approx 101{,}3 \Rightarrow 1{,}3 %$

Следовательно, оптимальная стратегия выглядит следующим образом. В понедельник утром относим деньги в банк и кладем на депозит. К вечеру у нас будет 102 фантика. Во вторник с каждого фантика мы можем заработать примерно 3,1 %; это больше, чем ставка по кредиту. Тогда во вторник утром мы возьмем в кредит у банка 102 фантика, и у нас будет 204 фантика. После этого с помощью арбитража мы заработаем $204 \times 1{,}031= 210{,}324$ фантика. Вечером банку нужно вернуть взятые в кредит деньги, а также вернуть 3 % за их использование. Тогда к концу вторника у нас останется $210{,}324-102 \times 1{,}03 \approx 210{,}324-105{,}06=105{,}264$ фантика. В среду, как и в понедельник, выгодно положить деньги на депозит. Тогда к концу среды
наш счет будет составлять примерно $105{,}264 \times 1{,}02 \approx 107{,}369$ фантика.

Отметим, что это не точное значение, а лишь его приближенная оценка. Чтобы получить точное значение, необходимо отказаться от всех округлений, которые мы совершали.

б) Здесь вариативность стратегий резко возрастает, так как появляется возможность брать кредиты и делать вклады в других валютах, нежели только фантики, и, самое важное, играть на обесценении валют в течение ночи.
Рассмотрим все возможные наборы стратегий.
Рассмотрим сначала операцию кредитования. Из пункта а) нам известно, что доходность от арбитража 1,8 %. Единственная кредитная ставка, которая меньше кредит по евро. Но на начало дня у нас на руках фантики, таки образом в первый день брать кредит не будем. Во вторник доходность арбитража 3,096 %. Это больше, чем кредит по любой из валют, и, таким образом во вторник при любой операции имеет смысл брать кредит. В среду самый маленький доход от арбитража, и потому брать кредит не имеет смысла.
Рассмотрим пока ситуацию, когда мы ни разу за три дня не клали деньги в банк.
Назовем профилем стратегии выбор валюты на руках в конце периода. Так как в среду мы в конце дня должны иметь на руках фантики, у нас 9 (=3*3) возможных профилей.

Стратегия	На руках в конце понедельника	На руках в конце вторника	На руках в конце среды
1	Ф*	Ф*	Ф*
2	Е*	Ф*	Ф*
3	S	Ф	Ф*
4	Ф*	E	Ф*
5	Е*	E*	Ф*
6	S	E*	Ф*
7	Ф*	S*	Ф
8	Е*	S	Ф
9	S	S*	Ф

Звездочками отмечены те позиции, при которых имеет место арбитраж. Арбитраж получается, когда мы делаем более одной операции в цепочке $Ф \to \$ \to € \to Ф \ $ для понедельника (т.е. мы получим больше, нежели просто переведем деньги в данную валюту прямым обменом; при одинаковой валюте в начале и конце дня прямой обмен означает отказ от операций с валютой), и $Ф \to € \to \$ \to Ф \ $ для вторника и среды
Осталось заметить еще одну вещь. Даже если во второй день по стратегии невозможен арбитраж (если мы закончили, например, понедельник с долларами, а вторник хотим закончить с фантиками), то кредит все равно имеет смысл брать. Поясним. Рассмотрим самый дорогой кредит в фантиках. При этом, поскольку мы хотим рассмотреть стратегию без арбитража, то предположим, что мы рассматриваем стратегию 8.
Взяв кредит на $Х$ фантиков под 3 % мы должны будем в конце дня вернуть $1{,}03Х$. В то же время мы на арбитраже заработаем $1{,}03096Х$. Таким образом, чтобы вернуть кредит, нам достаточно прокрутить $1{,}03/1{,}03096=0{,}99906X$. Оставшуюся сумму в $0{,}0009Х$ мы можем использовать по своему усмотрению, например, согласно стратегии 8 конвертировать в доллары. Т. е. конвертировать всю сумму наличных фантиков, включая кредитные, в евро, потом в доллары, а в фантики обернуть третьим шагом только сумму необходимую для погашения кредита.
Поскольку это работает для самого дорого кредита, эта стратегия верна и для более дешевых ставок.

Сопоставим изменения в относительной стоимости валют:

\textphi/€	43	$1{,}009302=43{,}4/43$	43,4	$0{,}993088=43{,}1/43{,}4$	43,1
\textphi/$	33	$0{,}99697=32{,}9/33$	32,9	$1{,}021277=33{,}6/32{,}9$	33,6
$/€	1,28	$1{,}0625=1{,}36/1{,}28$	1,36	$0{,}955882=1{,}3/1{,}36$	1,3

Исходя из этой таблицы, с понедельника на вторник выгодней всего хранить в евро (укрепился относительно и фантика и доллара), а со вторника на среду хранить деньги в долларах. Наименее выгодно заканчивать понедельник с долларами, а среду с евро.
Однако у этой стратегии есть недостаток два дня из трех придется работать без арбитража.
Рассмотрим каждую из 9 стратегий.

Стратегии 1, 4 и 7, согласно расчетам пункта а), уступают по доходности операции по вложению денег в банк в понедельник. Оставим рассмотрение аналога этих стратегий с вкладом до раздела с операциями по вкладам. Аналогичным образом в стратегиях 2 и 3 выгодней в среду положить деньги в банк.
Таким образом, осталось рассчитать доходность по стратегиям 5, 6, 8 и 9.

5: В конце понедельника имеем 2,3674 евро (только арбитраж). Во вторник берем кредит полностью крутим всю наличность опять до евро и гасим кредит. Остается 2,4785 евро. В среду арбитражем получаем 108,26 фантиков.
6: В конце понедельника без арбитража получаем 3,0303 доллара. Во вторник берем кредит на все доллары, крутим до евро, после этого конвертируем в доллары только сумму для погашения. Удвоив сумму, получим в евро $6{,}0606 \times 32{,}9/43{,}4= 4{,}5943$ евро, из которых $3,0303 \times 1{,}0225/1{,}36=2{,}2783$ нужно конвертировать в доллары и отдать на погашение кредита. Остается 2,316 евро. В среду арбитражем получим 101,1643 фантика.
8: В конце понедельника с арбитражем получаем 2,3674 евро. Операция с кредитом с евро позволяет вызволить $1-1{,}015/1{,}03096=0{,}01548$ от исходной суммы что составит 0,03665 евро. Вместе с исходными прямая конвертация в доллары даст $2{,}4041 \times 1{,}36=3{,}268$ доллара. В среду без арбитража получим 109,85 фантиков.
9: В конце понедельника без арбитража получаем 3,0303 доллара. Во вторник берем кредит и полностью прокручиваем. Получаем 3,1498 доллара, что меньше чем в стратегии 8.

Рассмотрим операции с вкладом. Отметим, что доходность арбитража во вторник (сопоставимо с вкладом, так как конечная и начальная валюта в обоих случаях совпадает) выше ставки вклада. Поэтому во вторник делать вклад не потребуется.
Рассмотрим упущенные стратегии 1, 2, 3, 4, 7 в предпосылке, что на некоторых шагах выгоднее делать вклад.

1: В понедельник имеем 102 фантика. Во вторник берем кредит, крутим получаем 102,2558. В среду опять кладем в банк и получаем 107,361.
2: В конце понедельника имеем 2.3674 евро. Берем кредит в евро, крутим до фантиков (211,8561), остаток для погашения кредита в размере $2,3674 \times 1{,}015=2{,}4029$ конвертируем в евро. Получаем на конец вторника 107,56 фантиков. В среду кладем в банк и получаем 109,72 фантика.
3: В конце понедельника без арбитража получаем 3,0303 доллара. Берем кредит в долларах все за один шаг превращаем в фантики (199,3939), а остаток для погашения крутим опять до долларов. В конце дня имеем 100,5158, что сильно хуже стратегии 2.
4: В понедельник имеем 102 фантика. Во вторник берем кредит, крутим до евро, остаток для погашения долга перекидываем до фантиков. На руках остается 2,3524 евро. Что меньше, чем в стратегии 5.
7: В понедельник имеем 102 фантика. Во вторник берем кредит, крутим до доллара, далее конвертируем сумму, необходимую для погашения кредита. На руках остается 3,1993 доллара. Что меньше, чем в стратегии 8.

Таким образом, наиболее выигрышной стратегией, как и было предсказано, является стратегия 8 с результатом 109,85.

Будем называть первым, вторым и третьим студентов, живущих на первом, втором и третьем этаже соответственно, через $x, y$ и $z$ будем обозначать их стратегии суммы, которые каждый из них потратит на уборку, а через $U_i(x,y,z)$ полезность $i$-го студента при условии, что первый потратил $x$, второй потратил $y$, а третий потратил $z$. Будем искать равновесные профили стратегий наборы $(x,y,z)$, такие, что ни один из студентов не захочет изменить свою стратегию при фиксированных стратегиях остальных студентов.
а) По условию каждый студент может профинансировать уборку любого целого числа этажей, поэтому $x,y,z \in {0,2,4,6}$.

1) Первому студенту не имеет никакого смысла оплачивать уборку более чем одного этажа, а второму больше двух. Поэтому в равновесии $x \in {0,2}$ и $y \in {0,2,4}$.

2) Профиль $(x,y,z)=(0,0,0)$ не является равновесием, поскольку второму студенту выгодно отклониться и профинансировать уборку одного этажа: $U_2(0,0,0)=12 < 16=U_2(0,2,0)$.

3) Профиль $(x,y,z)=(2,0,0)$ не является равновесием, поскольку третьему студенту выгодно отклониться и профинансировать уборку одного этажа: $U_3(2,0,0) = 16 < 17=U_3(2,0,2)$.

4) Из пунктов 13 следует, что профили, в которых $y=z=0$, не являются равновесиями. Значит, в равновесии хотя бы один из двух студентов второй или третий платит ненулевую сумму денег.

5) Студент, живущий на первом этаже, в равновесии не будет оплачивать ни одного этажа, если любой из живущих выше профинансирует хотя бы один этаж. Поэтому из $yz \neq 0$ следует $x=0$.

6) Из пунктов 45 следует, что в равновесии первый студент ничего не платит: $x=0$.

7) Рассмотрим случай $x=y=0$. Заметим, что $U_3(0,0,4)=15 > 14=U_3(0,0,2)=U_3(0,0,6) > 11=U_3(0,0,0)$. Значит, если первый и второй студенты не скидываются на уборщицу, то третий предпочтет оплатить помывку двух этажей.

8) Легко проверить, что $(0,0,4)$ равновесие. Это следует из пункта 7, а также из того, что первому и второму студенту не имеет смысла что-либо платить уборщице, когда третий студент оплатил уборку первых двух этажей.

9) Рассмотрим случай $x=0$, $y=2$. Заметим, что в равновесии $z \notin {4,6}$, так как в противном случае второй студент действует неоптимально, платя что-то в ситуации, когда третий студент уже оплатил уборку второго этажа.

10) Легко видеть (см., например, пункт 3), что $U_3(0,2,0)=16 < 17=U_3(0,2,2)$. Поэтому профиль $(0,2,0)$ не является равновесием.

11) Убедимся, что $U_2(0,2,2)=U_2(0,0,2)=18$. По условию в случае одинаково прибыльных альтернатив студент предпочитает ту, в которой он платит меньше. Значит, для второго студета профиль $(0,0,2)$ предпочтительнее профиля $(0,2,2)$. Из этого следует, что $(0,2,2)$ не равновесие.

12) Рассмотрим случай $x=0$, $y=4$. Заметим, что в равновесии $z=0$, так как в противном случае второй студент действует неоптимально, платя $y=4$. Но $U_2(0,4,0)=U_2(0,2,0)=16$, поэтому, в силу условия, второй студент предпочитает профиль $(0,2,0)$ профилю $(0,4,0)$. Следовательно, профиль $(0,4,0)$ не является равновесием.

13) Из пунктов 1 и 712 следует, что в пункте а) этой задачи есть ровно одно равновесие, когда третий студент оплачивает уборку двух этажей, а остальные студенты не платят ничего: $(x,y,z)=(0,0,4)$.

б)

1) Рассмотрим первого студента. Он может гарантировать себе полезность, равную как минимум 17, если не будет ничего платить.

2) В силу пункта 1 первый студент никогда не будет платить больше 2 долларов.

3) Первый студент будет оплачивать уборку одного этажа в том и только в том случае, если два других студента оплатили ровно два этажа (тогда полезность первого студента равна 18, в то время как грязный первый этаж принесет ему полезность не более 17).

4) Пусть $x=2$. Тогда, в соответствии с пунктом 3, $y+z=4$. Профиль $(2,0,4)$ не является равновесием, так как третьему студенту будет лучше уменьшить его долю до 2. Профиль $(2,2,2)$ не является равновесием, так как третьему студенту лучше вообще ничего не платить. Профиль $(2,4,0)$ не является равновесием, так как второму студенту выгоднее оплатить уборку только одного этажа (по условию задачи, если полезность одинакова, студент предпочтет тот вариант, в котором он платит меньше денег). Следовательно, в равновесии $x \neq 2$. Поэтому $x=0$.

5) Пусть $x=0$. Если $y+z=0$ или $y+z=2$, то это не равновесие, так как третьему студенту будет выгоднее профинансирвоать уборку еще одного этажа.

6) Если $x=0$ и $y+z=4$, то это не равновесие в силу пункта 3.

7) Пусть $x=0$ и $y+z=6$. Если $y=2$, $y=4$ или $y=6$, то второму студенту будет выгоднее изменить свое решение и уменьшить свои расходы на 2 доллара. Если $y=0$ и $z=6$, то третьему студенту выгоднее уменьшить свои расходы на 2 доллара.

Таким образом, в пункте б) нет равновесий.

в) а)

1) Очевидно, что первому студенту нет смысла финансировать помывку второго и третьего этажа. Поэтому $x \leqslant 3$.

2) Если $x>0$ и $x+y+z \neq 3$, то это не равновесие. Действительно, если $x+y+z > 3$, то первый студент мог бы сэкономить первый этаж и так будет помыт. А если $x+y+z < 3$, то первый студент выбрасывает деньги на ветер.

3) Заметим, что если $x+y+z=3$, то есть профинансирована уборка одного этажа, то независимо от распределения расходов студентов третьему студенту будет выгоднее доплатить еще 3 доллара за уборку оставшихся двух этажей (на этом он сэкономит 4 единицы неудовольствия). Значит, профили, такие, что $x+y+z=3$, не являются равновесиями.

4) Пусть $x=0$. Если $y+z=0$, то это не равновесие, так как третьему студенту будет выгоднее оплатить уборку первого этажа. Если $y+z \in {1,2,4}$, то этот профиль не является равновесием, так как второй или третий студент тратит деньги впустую. Если $y+z=3$, то это не равновесие по пункту 3).

5) Пусть $x=0$ и $y+z=5$. Легко непосредственной проверкой убедиться, что профили $(0,1,4)$, $(0,0,5)$ являются равновесиями. Профили, в которых $y\geqslant 2$, равновесиями не являются, так как второму выгодно уменьшить свой платеж на 2 (при том же уровне полезности он заплатит меньше).

6) Если $x=0$ и $y+z=6$, то равновесий нет: если $z>0$, то третьему выгодно уменьшить платеж на 1, а если $z=0$, то второй зря оплачивает уборку третьего этажа.

Таким образом, есть 2 равновесия: $(0,1,4)$ и $(0,0,5)$.

в) б)

1) Как и в пункте {б)}, первый студент никогда не будет платить больше 2 долларов.

2) Если первый студент тратит больше нуля, то в сумме оплачивается уборка всех этажей (иначе первому бы стало лучше, если бы он ничего не платил). Другими словами, если $x > 0$, то $x+y+z=6$.

3) Если $x+y+z=6$, то $z=0$. Действительно, если $z > 0$, то третьему студенту выгоднее потратить на 1 доллар меньше. Тогда первый этаж не будет вымыт, третий студент получит тот же уровень полезности, но заплатит меньше.

4) Если $x+y+z=6$, то $y \leqslant 1$. Если бы было $y > 1$, то второму студенту было бы выгодно уменьшить свой вклад на 2.

5) Из пунктов 24 следует, что равновесий в случае $x > 0$ быть не может. Следовательно, $x=0$.

6) Пусть $x=0$. Если $y+z < 3$, то это не равновесие, поскольку третьему студенту будет выгодно добавить столько денег, чтобы хватило на уборку двух верхних этажей. Если $y+z \in {4,5}$, то кто-то из студентов отдает уборщице деньги задаром. Случай $y+z=6$ не может быть равновесием в силу пунктов 3 и 4.

7) Остается случай $x=0$, $y+z=3$. Легко проверить, что все такие профили являются равновесиями. Сейчас убираются два этажа, и никому не выгодно увеличивать свой платеж на 3, чтобы оплатить уборку еще одного этажа. Уменьшать свой платеж второму или третьему нет никакого смысла штраф за грязь будет больше.

Таким образом, равновесия в этом пункте такие: $(0,0,3)$, $(0,1,2)$, $(0,2,1)$, $(0,3,0)$.

г) а) Суммарная полезность трех студентов в зависимости от числа вымытых этажей $n$ равна
$$
U(n)=60-3 \times(1-min(n,1))^2-2\times(2-min(n,2))^2-(3-min(n,3))^2-2n.
$$
Нам достаточно сравнить значения функции $U(n)$ при $0 \leqslant n \leqslant 3$. Легко видеть, что
$$
U(0)=40, U(1)=52, U(2)=55, U(3)=54.
$$
Таким образом, общественный максимум будет при двух мытых этажах. Суммарная полезность студентов по сравнению с равновесием из пункта а) не изменится.

г) б) Теперь суммарная полезность трех студентов в зависимости от числа вымытых этажей $n$ равна
$$
U(n)=60-3\times(1-max((n-2),0))^2-2\times(2-max((n-1),0))^2-(3-max(n,0))^2-2n.
$$
Вычислим значения функции $U(n)$ при $0 \leqslant n \leqslant 3$:
$$
U(0)=40, U(1)=43, U(2)=50, U(3)=54.
$$
Следовательно, общественно оптимальным вариантом является уборка трех этажей. Напомним, что в пункте б) равновесий не было!

г) в) а) В этом пункте суммарная полезность трех студентов может быть представлена в виде
$$
U(n)=60-3\times(1-min(n,1))^2-2\times(2-min(n,2))^2-(3-min(n,3))^2-a(n),
$$
где
$$
a(n) = \begin{cases}
0, & \text{если $n=0$};\\
3, & \text{если $n=1$};\\
5, & \text{если $n=2$};\\
6, & \text{если $n=3$}.\\
\end{cases}
$$
Тогда
$$
U(0)=40, U(1)=51, U(2)=54, U(3)=54.
$$
В силу предпосылки задачи, управляющая компания опять выберет мытье 2 этажей. Для обоих допустимых здесь равновесий из задачи в)а) суммарная полезность студентов не изменится.

г) n в) б) Наконец, здесь суммарная полезность трех студентов равна
$$
U(n)=60-3\times(1-max((n-2),0))^2-2\times(2-max((n-1),0))^2-(3-max(n,0))^2-b(n),
$$
где
$$
b(n) = \begin{cases}
0, & если \ n=0; \\
1, & если \ n=1; \\
3, & если \ n=2; \\
6, & если \ n=3.\\
\end{cases}
$$
Поэтому
$$
U(0)=40, U(1)=44, U(2)=51, U(3)=54.
$$
Значит, управляющая компания наймет уборщицу для мытья всех трех этажей. По сравнению с пунктом в) б), управляющая компания добилась улучшения общественного благосостояния.