1. Спрос и предложение
Способ 1 - аналитический
Спрос задаётся линейной функцией: $Q^d(p)=a-b\cdot p$, где $Q^d$ – величина спроса, $р$ – цена,$ a>0$ и $ b>0$ – некоторые параметры функции спроса.
Предложение задаётся линейной функцией: $Q^s(p)=c+d\cdot p$, где $Q^s$ – величина предложения, $р$ – цена, $c \text{ и } d>0$ – некоторые параметры функции предложения.
Ситуация дефицита возникает, если при заданной цене $Q^d > Q^s$. Так как при цене $р=67$ $Q>0$, то величина дефицита вычисляется по формуле:
$$Deficit(p)= Q^d(p) - Q^s(p)=a-b\cdot p-c-d\cdot p=(a-c)-(b+d)\cdot p$$
И при $р=67$:
$$Deficit(67)= Q^d(67) - Q^s(67)=a-b*\cdot 67-c-d \cdot 67=(a-c)-(b+d)\cdot 67=33 \textbf{ (1 балл)}$$
Ситуация излишка возникает, если при заданной цене $Q^s> Q^d$. Так как при цене $р=107$ $Q>0$, то величина излишка вычисляется по формуле:
$$Surplus(p)= Q^s(p) – Q^d(p)=c+d\cdot p-a+b\cdot p=-(a-c)+(b+d)\cdot p$$
И при $р=107$:
$$Surplus(107)= Q^s(107) – Q^d(107)=c+d\cdot 67-a+b\cdot 67=-(a-c)+(b+d) \cdot 107=11 \textbf{ (1 балл)}$$
Произведём замену переменных: $(a-c)=x, (b+d)=y $
Тогда получаем систему из двух уравнений с двумя неизвестными:
$$\begin{cases} x-67y=33 \\ -x+107y=11\end{cases} \Rightarrow \begin{cases}y=1,1 \\ x=106,7 \end{cases} \Rightarrow \begin{cases}b+d=1,1 \\ a-c=106,7\end{cases} \textbf{ (4 балла)}$$
При равновесной цене $(p^e)$ $Q^d=Q^s$, поэтому нет ни излишка, ни дефицита. Таким образом, в точке $p^e$ значения этих функций равны нулю:
$106,7 – 1,1\cdot p^e=0$ (1 балл)
$p^e=\dfrac{106,7}{1,1}=97$ (3 балла)
Способ 2 - геометрический
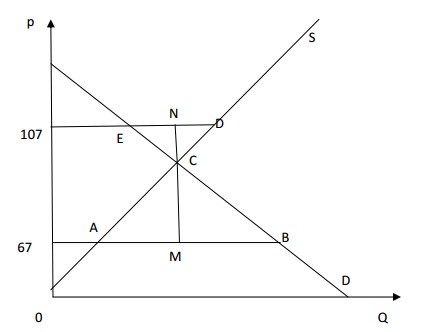
При решении данным способом обязательно наличие графика.
В данном случае отрезок AB отображает величину дефицита при цене 67 и его длина равна 33. Отрезок DE отображает величину излишка при цене 107, и его длина равна 11 (график, на котором указаны все нужные параметры, оценивался в 4 балла).
Треугольники ABC и DEC являются подобными. (1 балл)
Это означает, что коэффициент подобия треугольников равен соотношению подобных сторон, а именно: $k=\dfrac{AB}{DE}=\dfrac{33}{11}=3$ (1 балл)
Это означает, что высоты CM и CN данных треугольников соотносятся также как 3:1.
Длина отрезка MN равна $107–67=40$. Обозначим длину отрезка CN за $z$. Тогда получаем следующее уравнение:
$$\begin{array}{l}3z+z=40 \\ z=10 & \textbf{(1 балл)} \end{array}$$
Получаем, что равновесная цена равна $107-10=97$ рублей. (3 балла)
2. Товар Х
Обратные функции спроса и предложения можно записать следующим образом:
$$\begin{array}{l} P=100-0,25Q \\ P=20+0,25Q+t \end{array}$$
Приравняв их друг к другу, находим равновесное количество товара, как функцию от ставки налога: $Q^*=160-2t$ (3 балла)
Суммарные поступления в государственный бюджет равны: $tQ=160t-2t^2$. (1 балл)
Это парабола с ветвями, направленными вниз, следовательно, в точке вершины этой параболы поступления в государственный бюджет максимальны. (1 балл за это рассуждение. Если точка ищется с использованием производной, то также должно быть показано, что это точка максимума).
Найдя вершину, получаем: $t^*=40$ (1 балл)
Теперь можно получить соответствующее равновесное количество: $Q^*=160-2t^*=80$
После этого получаем искомую равновесную цену: $P^*=100-0,25\cdot 80$ (3 балла)
3. Монополия
Во всех остальных точках предельный доход меньше предельных издержек (4 балла, этот факт может быть показан путем решения соответствующего неравенства ИЛИ путем аккуратного изображения графиков $MR \text{ и } MC$ на одном рисунке).
Следовательно, прибыль фирмы убывает (не возрастает в точке $q=3$) с увеличением объёма выпуска. Поэтому наилучшим решением для фирмы будет нулевой объём выпуска. (4 балла)
4. "Сигма" и лицензия
В первом случае она получит прибыль равную $PR(0)=-8$ (1 балл)
Во втором случае её прибыль составит: ܲ$PR=P\cdot Q-\dfrac{q^2}{200}-8-50$ (1 балл)
Относительно объёма выпуска это парабола с ветвями, направленными вниз, следовательно, вершина этой параболы будет соответствовать максимальной прибыли.
Найдем её: ܳ$Q^*=100P$. Прибыль при данном объёме выпуска составит: $$\begin{array}{l} PR(Q^*)=P\cdot 100P-\dfrac{(100P)^2}{200}-8-50 \\ PR(Q^*)=50P^2-8-50 & \textbf{ (2 балла)}\end{array}$$
Ясно, что фирма согласится выбирать положительный объём выпуска только в том случае, если прибыль от этого варианта не меньше, чем от нулевого. Иными словами, только в том случае, если: $PR(Q^*) \geq PR(0)$ (3 балла за идею сравнения прибылей)
$$\begin{array}{l} 50P^2-8-50 \geq -8 \\ P \geq 1 & \textbf{ (3 балла)}\end{array}$$